这个知识点每年都考！你咋还不会？！

今天艾老师要给同学们讲讲“两期比例”问题，其实这类题就是套路题，与混合增长率一样，知道口诀就会做。但大家也别小瞧了这个知识点，考察的频率可是不低呢，两期平均数中的平均数的增长率这一考点更是每年国考必考，学会了就是稳拿分，快来和我一起看看吧。

【知识点：两期比重的比较】

1、举例说明

2018年，山东省工业用电量占全国工业用电总量的比重与去年相比：

A.上升 

B.下降

C.不变 

D.无法判断

答：题干部分出现“2018年、比重、去年相比”，结合选项上升/下降/不变/无法判断，判定为两期比重比较问题，只要出现两个时间节点，并且比重做比较，就是两期比重比较问题。2018年比重-2017年比重＞0，则比重上升，2018年比重-2017年比重＜0，则比重下降。

2、题型识别

两个时间+比重（上升/下降）

3、解题方法

只需比较a与b的大小关系，在资料分析中，部分量用A表示，总体量用B表示，a对应分子部分的增长率，b对应分母部分的增长率。

（1）a＞b，比重上升。

（2）a＜b，比重下降。

（3）a=b，比重不变。

4、推导过程

现期比重- 基期比重=A/B-A/B*[（1+b）/（1+a）]=A/B*[（a-b）/（1+a）]=A/B*[1/（1+a）]*（a-b），A/B和1/（1+a）都是正数，则两者相乘也是正数，这个式子的正负取决于（a-b）的正负，如果a＞b，则式子＞0，比重上升；如果a＜b，则式子＜0，比重下降。

【注意事项】

a可能为正数，也有可能为负数，但是下降率是默认有前提的，假设去年是100万，今年是0，则减少了100%，即1+a最小为0，不可能为负数，所以1/（1+a）＞0。

【例1】

2017年，全省全年完成快递业务量100.51亿件，同比增长31.0%。其中，同城快递业务量增长29.3%，异地快递业务量增长33.0%，国际和港澳台地区快递业务量增长33.1%。2017年A省快递业务中，业务量占总业务量比重高于上年水平的分类是：

A.仅国际和港澳台地区快递    

B.异地快递、国际和港澳台地区快递

C.仅同城快递  

D.同城快递、异地快递

【解析】

先判定题型，出现比重，要求2017年的比重高于上年水平，判定为两期比重比较问题，要求比重高于上年水平，即比重上升，要满足a＞b，找a和b的关系即可。a是分子的增长率，b是分母的增长率，b=31.0%，同城快递a1=29.3%，异地快递a2=33.0%，国际港澳台快递a3=33.1%，即异地快递和国际港澳台快递满足，对应B项。【选B】

【例2】

2016年该市本级完成财政一般预算支出49.86亿元，比上年增支16.79亿元，增长50.8%。

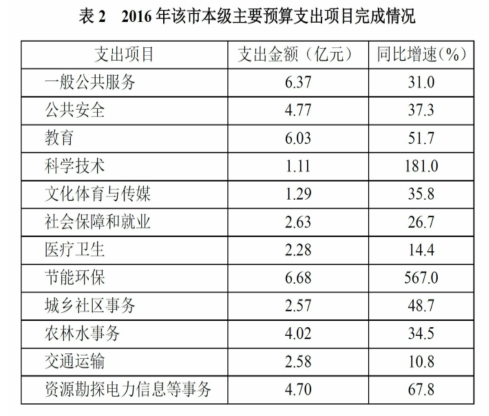
2016年该市本级主要预算支出项目中，占总预算支出比重较上年有所提高的项目个数有：

A.7个 

B.6个

C.5个 

D.4个

【解析】

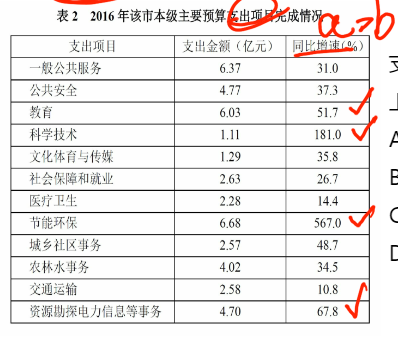
出现比重，要满足比重上升，即要满足a＞b，找出a和b比较即可，a是部分量的增长率，b是总体量的增长率，先找总体量的增长率，b=50.8%，a对应各个支出项目的增长率，观察发现有4个项目满足，对应D项。【选D】

【知识点：两期比重的计算】

1、举例说明

2018年，山东省园区企业上缴税金占主营业务收入的比重比上年：

A.上升了0.1个百分点 

B.上升了3.1个百分点

C.下降了0.1个百分点 

D.下降了3.1个百分点

答：要求具体上升/下降了几个百分点，需要计算出来，是两期比重计算问题，出现两个时间+上升/下降+百分点，就是两期比重计算问题。假设a＞b，则判定为上升，排除C、D项。

2、题型识别

两个时间+比重（上升/下降几个百分点）。

3、解题方法

（1）判方向：a＞b，比重上升；a＜b，比重下降。

（2）定大小：结果小于|a-b|。

4、推导过程

A/B*[（a-b）/（1+a）]=A/B*[1/（1+a）]*（a-b）＜|a-b|，A/B是一个比1小的值，1/（1+a）分两种情况，如果a＞0，1+a＞1，则1/（1+a）＜1，则1-*1-*（a-b）＜|a-b|；如果a＜0，1+a＜1，则1/（1+a）＞1，在数学中存在这种情况，但是资料分析的数据都是从统计局摘选出来的，我国的经济一直在持续稳定增长，所以1/（1+a）≈1，则1-*（≈1）*（a-b）＜|a-b|，过程不需要理解，记住结论即可。

【例3】

2014年1～5月，我国软件和信息技术服务业实现软件业务收入13254亿元，同比增长20.9%……

1～5月，东部地区（不含东北地区）完成软件业务收入10254亿元，同比增长20%，中部完成软件业务收入491亿元，同比增长28.8%，西部和东北地区分别……

问，2014年1～5月中部地区完成软件业务收入占全国的比重与2013年同期相比上升了约多少个百分点？

A.0.2  

B.1.9

C.4.7  

D.7.9

【解析】

出现“谁占谁的比重”，问2014比2013年上升几个百分点，为两期比重的比较问题。考查年份的比较占比达到90+%，极个别的情况会考查季度比较和月份比较，很少考，基本都是年份的比较。本题不用判方向，题干已知是上升，直接定大小即可。定位材料找数据，中部地区增长率a=28.8%，全国增长率b=20.9%，结果小于|a-b|=|28.8%-20.9%|=7.9个百分点，只能排除D项；A项0.2可以看成0.19，和B项1.9存在量级差异，计算的时候要注意数位和单位，此时大大增加了计算难度，建议直接选最小，对应A项。【选A】

【知识点】

1、题型识别

两个时间+比重

2、计算公式

A/B*[（a-b）/（1+a）]

3、解题步骤

（1）判方向：a＞b，上升；a＜b，下降

（2）定大小：小于|a-b|

4、注意事项

（1）若选项中只有一个小于|a-b|，直接选即可。

（2）若选项中有多个小于|a-b|：

①时间充足代入公式计算。

②时间紧张猜最小（90%正确率）：除了广东（考的是间隔两期比重，与常规的相邻两个年份的两期比重不同）和新疆出现过反例，在国考中无一例外。

【知识点】

两期比重的逆运用：前面的题目都是给出a和b，比较a和b的大小关系来判断比重上升/下降/不变（a＞b，比重上升；a＜b，比重下降；a=b，比重不变），同时也可以根据比重上升/下降/不变来判断a和b的大小关系。

1、a＞b⇔比重上升。

2、a＜b⇔比重下降。

3、a=b⇔比重不变。

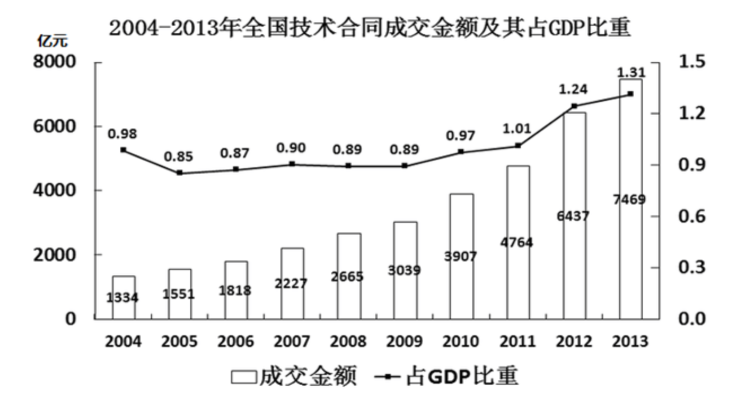
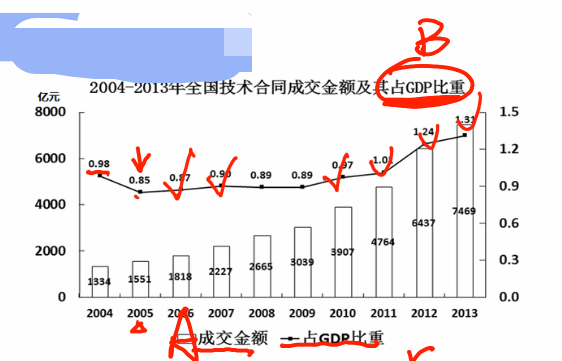
【例4】2005～2013年，全国技术合同成交金额增速超过GDP增速的年份有（  ）个？

A.3    

B.4

C.5    

D.6

【解析】

没有给成交金额的增速，也没有给GDP的增速，只给了成交金额占GDP的比重变化，部分量A（a）对应成交金额，总体量B（b）对应GDP，要想求a＞b的年份有几个，直接看占比上升的年份有几个（比重上升→a＞b），定位折线图，2005年：从0.98到0.85，比重下降，排除；2006年：从0.85到0.87，比重上升，满足；同理，比重上升的年份有：2006年、2007年、2010年、2011年、2012年、2013年，共有6个年份，对应D项。【选D】

【注意】

本题难点在于题型判定，需要课下多做练习和总结，提高敏感性。

【知识点】

两期平均数的比较：和两期比重的比较是完全一致的，因为都可以表示为A/B的形式，若将A/B看成平均数，则分子为总体（增长率为a），分母为份数（增长率为b）；若将A/B看成比重，则分子为部分（增长率为a），分母为总体（增长率为b）。形式一致，则计算、比较方法和推导过程也一致。

1、题型识别

两个时间+平均数（上升/下降）

2、升降判断

a：分子部分的增长率，b：分母部分的增长率。

（1）a＞b，平均数上升。

（2）a＜b，平均数下降。

（3）a=b，平均数不变。

【例1】

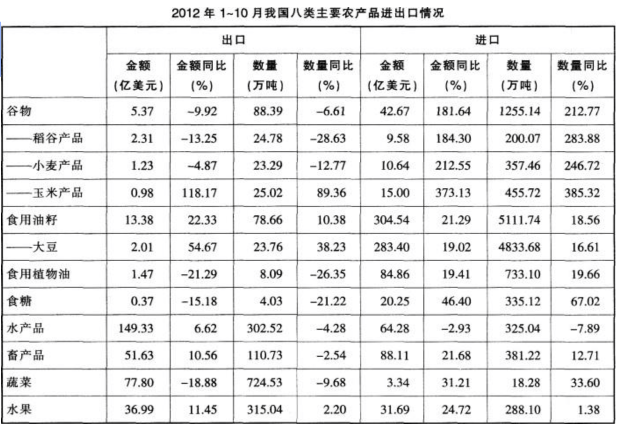
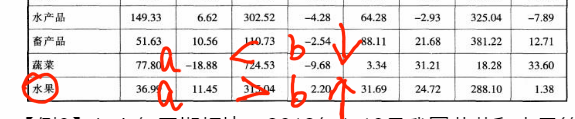
与上年同期相比，2012年1～10月我国蔬菜和水果的平均出口单价：

A.均有所提高  

B.均有所下降

C.只有蔬菜价格提高   

D.只有水果价格提高

【解析】

出现“与上年同期相比”，一定是两期问题；比较的是平均出口单价，为平均数；选项出现提高/下降，故本题为两期平均数的比较问题，直接比较a和b的大小关系。平均出口单价=金额（a）/数量（b），注意问的是出口，不要看进口。定位表格找数据，蔬菜：a（-18.88%）＜b（-9.68%），平均数下降；水果：a（11.45%）＞b（2.20%），平均数上升。一个提高，一个下降，排除A、B项；只有水果价格提高，对应D项。【选D】

【知识点：两期平均数的计算】

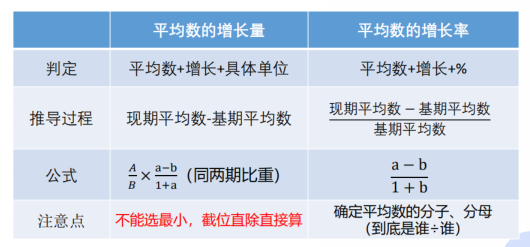
1、平均数的增长量：

（1）判定：平均数+增长+具体单位（如万元/家/个），即求某个主体的增长量，但这个主体是一个平均数，如平均每家企业的收入增长多少万元。

（2）推导过程：现期平均数- 基期平均数。

（3）公式：A/B*[（a-b）/（1+a）]（同两期比重）。

（4）注意点：不能选最小，截位直除直接算。

2、平均数的增长率（国考每年必考）：

（1）判定：平均数+增长+%，如平均每家企业的收入增长了百分之多少。

（2）推导过程：（现期平均数- 基期平均数）/基期平均数。

（3）公式：（a-b）/（1+b）。

（4）注意点：确定平均数的分子、分母（到底是谁除以谁）。   

【例2】

2017年，A省完成客运总量148339万人次，同比增长5.4%，增幅比前三季度提高0.2个百分点，比上年提高0.5个百分点；完成旅客周转总量4143.84亿人公里，增长7.7%，增幅比前三季度提高0.7个百分点，比上年提高1.8个百分点。问，2017年前三季度，A省平均每人次客运旅客运输距离（旅客周转量÷客运总量）同比：

A.下降了不到2%   

B.下降了2%以上

C.上升了不到2%   

D.上升了2%以上

【解析】

同比上升/下降，求增长率，主体是平均每人次客运旅客运输距离，求平均数，为平均数的增长率问题。a对应分子增长率，b对应分母增长率，r=（a-b）/（1+b），平均每人次运输距离=运输距离/人次。要注意资料分析中，时间和主体必须要把握精确，高减低加，a=7.7%-0.7%=7%，b=5.4%-0.2%=5.2%，则r=（7%-5.2%）/（1+5.2%）≈1.8%/1.05，不要计算，先看选项，1.8%除以比1大的数，一定小于1.8%，且是一个正值，意味着上升，排除A、B项；数值小于1.8%，对应C项。【选C】

【例3】

2012年，某省加大扶持贫困残疾人力度，财政投入扶贫资金3816.3万元，比上年大幅增长18%，扶持贫困残疾人员56561人，脱贫35110人，享受优惠政策的贫困残疾人117727人，比上年增加3%。该省每年投入的残疾人财政扶贫资金如果可以均分到每位享受优惠政策的贫困残疾人身上，则2012年享受优惠政策的贫困残疾人的人均扶贫金额要比2011年增长约（  ）元。

A.30   

B.40

C.50   

D.60

【解析】

增长+单位，求增长量，且求的是人均，本题为平均数的增长量问题。公式为A/B*[（a-b）/（1+a）]，若选项差距比较小且存在量级陷阱，则需要注意位数和具体值。选项都是两位数，没有量级陷阱，忽略量级计算，代入公式：38/12*[（18%-3%）/（1+18%）]，保留两位，（38/12）*（15/12）=38*15/144，将38*15/144看成38*1+，38*1+，选比38略大一点点的数，对应B项。【选B】

【注意】

也可以化简计算：（38/12）*（15/12）=（38/12）*（5/4）=（38*5）/48=38*1+＞38，选比38略大一点点的数。

1、两期平均数的比较：和两期比重完全一致。

（1）a＞b，平均数上升。

（2）a＜b，平均数下降。

（3）a=b，平均数不变。

2、平均数的增长率+平均数的增长量：

（1）平均数的增长量：联考偶尔考。

①判定：平均数+增长+具体单位。

②公式：A/B*[（a-b）/（1+a）]（同两期比重）。

（2）平均数的增长率：国考必考，更为重要。

①判定：平均数+增长+%。

②公式：（a-b）/（1+b）。